Aplikasi Teori Graf

Ada beberapa aplikasi teori graf salah satunya yaitu pewarnaan graf (graph colouring). Ada beberapa macam pewarnaan graf yaitu pewarnaan simpul, pewarnaan sisi, dan pewarnaan wilayah (region). Pada tulisan ini, kami akan membahas mengenai pewarnaan simpul pada graf.

Salah satu contoh dari aplikasi teori graf yaitu pewarnaan graf, khususnya pewarnaan simpul pada graf yaitu

Jarak Minimum Pemancar Radio Agar Tidak Terjadi Interferensi

Untuk mencari jarak minimum pemancar radio agar tidak terjadi interferensi yaitu dengan menggunakan algoritma powell-welch.

Algoritma Powell-Welch

Algoritma ini merupakan suatu langkah yang digunakan dalam pewarnaan graf. Algoritma ini terdiri dari beberapa langkah, yaitu (Munir, 2008):

1. Urutkan simpul-simpul dari graf dalam derajat yang menurun (urutan seperti ini mungkin tidak unik karena beberapa simpul mungkij berderajat sama).
2. Gunakan satu warna untuk mewarnai simpul pertama (yang mempunyai derajat tinggi) dan simpul-simpul lain (dalam urutan yang berurut) yang tidak bertetangga dengan simpul pertama ini.
3. Mulai lagi dengan simpul derajat tinggi berikutnya di dalam daftar terurut yang belum diwarnai dan ulangi proses pewarnaan simpul dengan menggunakan warna
4. Ulangi penambahan warna-warna sampai semua simpul telah diwarnai.

Penerapan Algoritma Powell-Welch dalam Pengaturan Frekuensi Radio

Ketimpangan antara persediaan spektrum frekuensi radio gelombang dan peningkatan jumlah stasiun radio menjadi salah satu permasalahan yang muncul, seperti yang terjadi di Provinsi Daerah Istimewa Yogyakarta. Untuk itu diperlukan manajemen radio frekuensi unit dalam rangka menghindari terjadinya interferensi gelombang transmisi antara dua atau lebih stasiun radio. Persoalan ini dapat dikaji pengaturannya menggunakan prinsip pewarnaan simpul. Untuk lebih jelasnya berikut adalah langkah-langkah aplikasi pewarnaan simpul pada unit frekuensi radio yang diadaptasi dari Mussafi (2013):

1. Menyajikan data kuat medan listrik antara sebarang dua titik (dalam hal ini sebarang dua radio yang berbeda).
2. Mentransformasi stasiun radio beserta garisnya ke bentuk graf. Seperti yang telah dijelaskan pada landasan teori, graf terdiri atas simpul dan garis. Simpul merepresentasikan semua lokasi stasiun radio dan garis merepresentasikan dua sebarang stasiun radio yang saling terinterferensi yaitu jika E > 3,5 N/C yang selanjutnya simpul-simpul tersebut saling dihubungkan.
3. Mewarnai setiap simpul pada graf dengan menggunakan algoritma Powell-Welch. Selain untuk mengetahui stasiun radio mana saja yang diperbolehkan dalam satu kanal, diperoleh juga jumlah bilangan kromatik yang akanberguna pada tahap berikutnya.
4. Menentukan alternatif penyelesaian manajemen unit frekuensi radio dengan menyajikan dalam graf berwarna.

Berikut disajikan data mengenai kuat medan listrik antara dua sebarang stasiun radio di Daerah Istimewa Yogyakarta dengan mengambil data sampel 10 stasiun radio secara acak yang dikutip dari tulisan Mussafi (2013).

TABEL 1. kuat medan listrik dua sebarang radio (dalam satuan N/C)

Langkah-langkah penyelesaian alternatif manajemen unit frekuensi radio di Provinsi Daerah Istimewa Yogyakarta adalah sebagai berikut:

1. Berdasarkan studi literatur diperoleh data mengenai kuat medan listrik antara dua sebarang stasiun radio di wilayah Daerah Istimewa Yogyakarta, Data tersebut dapat dilihat pada tabel.
2. Transformasi stasiun radio beserta garis yang terhubung ke dalam graf. Stasiun radio dalam hal ini disebut sebagai titik dalam graf, sedangkan garis dipengaruhi oleh tingkat interferensi antara pasangan stasiun radio.

Data pada tabel diatas menunjukkan kuat medan listrik antara satu radio dengan lainnya yang dikatakan saling terinterferensi jika nilainya (J.H. Kraus, dalam Mussafi 2013). Dengan kata lain, untuk setiap kuat medan listrik maka tidak ada garis yang menghubungkan antara pasangan stasiun radio, sebagai contoh stasiun Sasando dan I-Radio memiliki nilai E = 1.33 N/C.

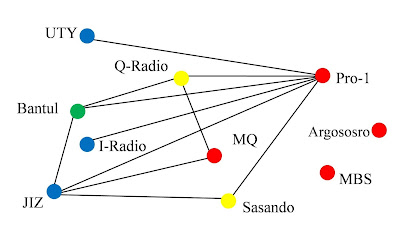
Sehingga berdasarkan data pada tabel 1 dapat dibuat representasi grafnya (lihat gambar 1).

Gambar 1. Representasi Graf Berbasis Interferensi Gelombang.

Pewarnaan simpul menggunakan algoritma Powell-Welch berdasarkan data pada gambar 1. Diawali dengan mengurutkan simpul-simpul dari graf G dalam derajat yang terbesar, seperti pada tabel berikut

TABEL 2. Simpul Graf diurutkan menurun berdasarkan derajatnya

Selanjutnya, menentukan satu warna yaitu merah untuk mewarnai simpul pertama dengan derajat terbesar yaitu Pro-1 dan simpul-simpul lain yang tidak berhubungan langsung dengan simpul Pro-1 yaitu MQ, MBS, dan Argososro.

Gambar 2. Pewarnaan Simpul dengan Derajat Terbesar pada Representasi Graf Berbasis Interferensi Gelombang

Dilanjutkan pewarnaan simpul biru untuk derajat tertinggi berikutnya yaitu JIZ dan simpul-simpul lain lain yang tidak berhubungan langsung dengan simpul JIZ yaitu UTY dan I-Radio.

Gambar 3. Pewarnaan Simpul dengan Derajat Terbesar pada Representasi Graf Berbasis Interferensi Gelombang

 dilanjutkan dengan pewarnaan simpul hijau untuk derajat tertinggi berikutnya yaitu Bantul, karena semua simpul yang tersisa bertetangga dengan simpul Bantul sehingga pewarnaan hanya pada simpul Bantul.

Gambar 4. Pewarnaan Simpul dengan Derajat Terbesar pada Representasi Graf Berbasis Interferensi Gelombang

Dilanjutkan dengan pewarnaan simpul kuning untuk derajattinggiberkutnya yaitu, Q-Radio dan simpul-simpul lain yang tidak berhubungan langsung dengan simpul Q-Radio yaitu Sasando.

Gambar 5. Distribusi Frekuensi Radio

Berdasarkan penggunaan algoritma Powell-Welch maka ilustrasi warna pada graf tersebut dapat dilihat padaa gambar 5. 

Misalkan simpul menyatakan suatu pemancar radio dengan frekuensi tertentu, dan sisi yangmenyatakan pemancara yang masih berada dalam jangkauan, dengan kata lain bertetangga. Pemancar Pro-1 dengan frekuensi "Merah" diharapkan akan memiliki frekuensi yang sama dengan pemancar MBS, Argososro dan MBS. Karena meskipun frekuensinya sama, tidak akan mengganggu siaran keempatnya tidak bertetangga (tidak berada dalam jangkauan satu sama lain), begitupula dengan warna lainnya. Sehingga, ada empat kelompok radio yang dapat memiliki frekuensi yang sama, seperti pada tabel berikut

TABEL 3. Kelompok Radio yang dapat Memiliki Frekuensi Sama

Inilah salah satu contoh aplikasi dari teori graf.
Mudah-mudahan dapat membantu teman-teman sekalian dalam memahami pewarnaan graf :).
Contoh ini saya peroleh dari salah satu tulisan yang berjudul Penerapan Pewarnaan Graf Dalam Penggunaan Frekuensi Radio. Tulisan yang saya peroleh ini sangat bermanfaat sekali buat saya karna dengan tulisan ini saya dapat menyelesaikan salah satu tugas final saya pada mata kuliah Matematika Diskrit II, dan Alhamdulillah hasilnya baik :). Dan pada kesempatan kali ini, saya sedikit share mengenai garis besar dari tulisan tersebut, dan mungkin sebagian besar dari isi blog ini adalah isi tulisan tersebut. Adapun kalau ada yang berbeda mungkin dari segi gambar dan tabel terakhir dari blog ini.

Daftar Pustaka dari tulisan Penerapan Pewarnaan Graf Dalam Penggunaan Frekuensi Radio

 

Sumber:

Alfiansyah, Muh., dkk. 2015. Penerapan Pewarnaan Graf Dalam Penggunaan Frekuensi Radio. [online], (https://webcache.googleusercontent.com/search?q=cache:06ONBn7VoxYJ:https://www.slideshare.net/MuhammadAlfiansyah1/penerapanan-pewarnaan-graf-dalam-penggunaa-frekuensi-radio+&cd=1&hl=en&ct=clnk&gl=id, diakses  24 mei 2018).